What Is the Centre of Gravity? What Is a Moment?
The Basics of Mechanical Design

How to Approach Centre of
Gravity and Moments

What Is the Centre of Gravity?

It is a point within an object where its mass can be considered to be concentrated.

What Is a Moment?

It is a measurement of the force required to rotate something along an axis.

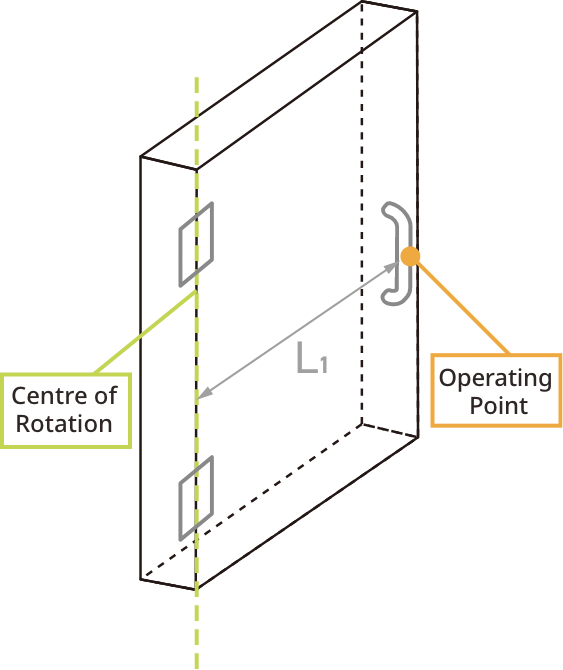
Door's Centre of Gravity

If a lid or door is a uniform shape, its centre of gravity is in the middle, as shown in the diagram. In other words, X1=L1÷2.

  • Please note: This is the reason our catalogues have used the formula L1÷2 up to now.
  • Please note: This formula applies to thin lids or doors.

Formula for Calculating Torque

Lid/door moment M
=
Horizontal distance from centre of rotation to centre of gravity X1
×
Mass m

The moment is calculated based on the horizontal distance to the centre of gravity. Because this value changes depending on the opening angle, the formula for calculating the maximum moment is as follows.

Maximum Lid/Door Moment
=
Maximum horizontal distance
from centre of rotation
to centre of gravity
×
Mass

Key Points When Selecting Hinges and Stays

Free Stop

  • If the torque of a hinge or stay is greater than the moment of the lid or door, it will free-stop.
  • It is best to bring the moment of the lid or door and the torque of the hinge or stay as close as possible, as this makes operation feel lighter.
Hinge (stay) torque*
≧
Maximum Lid/Door Moment

* When using multiple hinges or stays, multiply the torque value by the number of units

Damper (Soft Motion)

Maximum Hinge / Stay Torque*
≧
Maximum Lid/Door Moment
≧
Minimum Hinge / Stay Torque*

* when using multiple hinges or stays, the torque value will be multiplied by the number of units used.

Calculating Centre of Gravity for Complex Shapes

How to Determine the Centre of Gravity of Complex Shapes

When a lid is L-shaped or has an otherwise non-standard shape, divide it into simpler shapes, calculate the centre of gravity for each part, and determine the overall centre of gravity from the total of these. The same principle applies when attaching a mirror to a wooden panel.

Let's work through an example by dividing the shape into two parts

Lid Section A Centre of Gravity G1

Length L1*
cm
Thickness t1*
cm
Mass m1*
kg
Distance from centre of gravity G1 in the X direction X1
cm
Angle formed with centre of gravity G1
°
Distance from centre of gravity G1 in the Y direction Y1
cm
Moment of section A in X direction
kgf・cm
Distance to centre of gravity G1
cm
Moment of section A in Y direction
kgf・cm
  • * Input as negative figures if located on the negative side from centre of rotation.
  • * To simplify calculations, notation and input units have been changed from mm to cm.

Lid Section B Centre of Gravity G2

Length L2*
cm
Thickness t2*
cm
Mass m2*
kg
Distance from centre of gravity G2 in the X direction X2
cm
Angle formed with centre of gravity G2
°
Distance from centre of gravity G2 in the Y direction Y2
cm
Moment of section B in X direction
kgf・cm
Distance to centre of gravity G2
cm
Moment of section B in Y direction
kgf・cm
  • * Input as negative figures if located on the negative side from centre of rotation.
  • * To simplify calculations, notation and input units have been changed from mm to cm.

Total centre of gravity G

Total mass
kg
Centre of gravity in X direction
cm
Centre of gravity in X direction
mm
Centre of gravity in Y direction
cm
Centre of gravity in Y direction
mm
Distance to total centre of gravity
cm
Distance to total centre of gravity
mm
Angle formed with total centre of gravity
°

Please note: decimal points below the third are rounded up.

Cases Where Centre of Gravity is Unknown

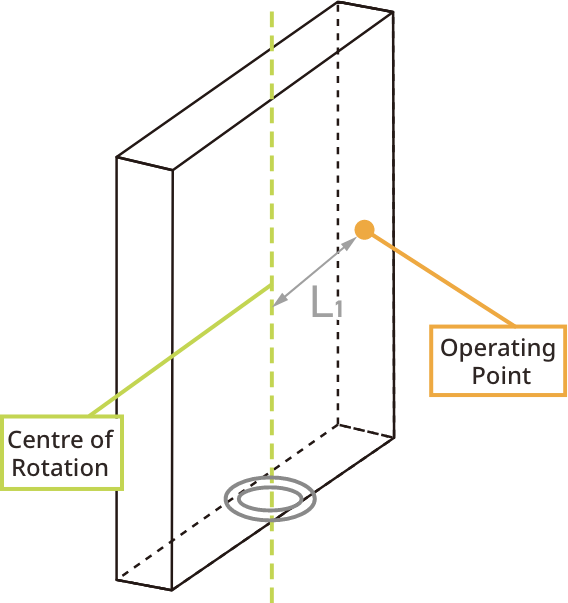
If a lid or door is already installed and its centre of gravity cannot be calculated, there is still a way to determine the required torque by using a spring scale.
As shown in the diagram, a spring scale is used to measure the maximum value when lifted up, and the distance from the centre of rotation to the measurement position.

L1
×
F1
=
Lid/Door Moment
L1
×
Maximum value of F1
=
Maximum Lid/Door Moment

Please note: when items of equipment are attached to a lid, this can make it difficult to calculate the centre of gravity.
In these cases, estimate the approximate weight and centre of gravity and make a provisional choice of hinge or stay.
After assembly, using the above method will confirm the precise torque value required, allowing you to select a permanent hinge or stay.

Example

With a distance (L1) of 100cm and a force (F1) of 2.5kg, applying the moment calculation formula results in a lid/door moment of 100cm x 2.5kg = 250kgf·cm.
Implementing free stop on this lid or door, for example, would require a hinge (stay) with a torque value of 250kgf·cm (equivalent to 24.5N·m) or more.
This means the hinge (stay)'s torque value is ≧ 250kgf·cm (= 24.5 N·m).

Let's run the calculation

Distance from centre of rotation to measurement position L1
cm
Force value measured with spring scale F1
kg

Lid/door moment = L1 x F1 x 9.80665 ÷ 100

N·m

Solve complex moment calculations with our selection tool!
Also simulates operating force!

Use our MDT Selection Tool to choose products that suit your needs,
just by entering the distance to the centre of gravity and the mass of the lid.

Click here to select products
Check the drawing
Check
the drawing

Loading